We introduce a powerful technique to transform all existing two-level quantum control methods to new multi-level quantum control methods. We illustrate the technique by coherently mapping between two different qubit types with error well below the relevant fault-tolerant threshold, creating another important tool towards constructing a large scale quantum computer. Manuscript published in Physical Review A.
Manuscript: Generation of high-fidelity quantum control methods for multi-level systems
INTRODUCTION
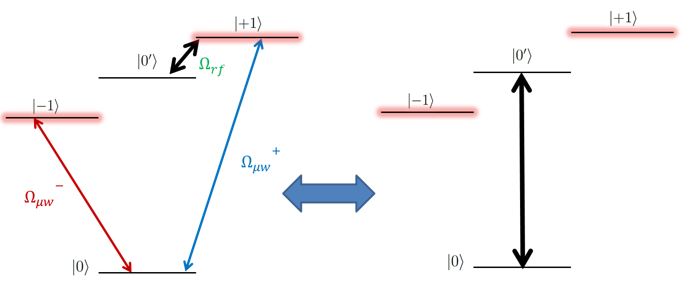
Quantum control methods are essential in many areas of experimental quantum physics, including trapped atoms, ions and molecules, and solid state systems [1–3]. Although the focus is often on two-level systems, in nearly all experimental realizations a larger number of states need to be taken into consideration, for example, to prepare a qubit in a two-level subspace of the system or to read out the state at the end of an experiment. In addition, the unique features of multilevel systems have led to new fields of research, including electromagnetically induced transparency [4] and single-photon generation [5]. Multilevel systems are also widely used in quantum computing, with applications such as the preparation and detection of dressed-state qubits [6,7]. A variety of multilevel methods including stimulated Raman adiabatic passage (STIRAP) [8], multistate extensions of Stark-chirped rapid adiabatic passage (SCRAP) [9], and other adiabatic methods involving chirped laser fields [10–12] have been developed, in addition to numerical algorithms for optimized quantum control [13]. However, the development of new control methods for multilevel systems (especially for high-fidelity operations) is challenging and often inhibited by the mathematical complexity of such higher-dimensional Hilbert spaces. Previous investigations into multilevel dynamics have studied coherent excitation of multilevel systems under the action of SU(2) Hamiltonians [14–18]. They showed that for a Hamiltonian with this symmetry there exists an equivalent Hamiltonian acting on a two-level system, and the dynamics of this twolevel Hamiltonian can then be used to find solutions for the dynamics of the higher-dimensional system.