Machine Learning - Lecture 15 Support Vector Machines
Chris Thornton
Introduction to max-margin classifiers
If there is a line (hyperplane) separating two sets of
datapoints, we can use error-correction to work
out what it is (see previous lecture).
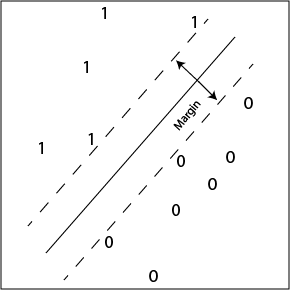
Another approach involves maximizing the weight-vector's
`safety margin', i.e., its inner product with the most
nearly mis-classified datapoint.
This gives us the so-called maximum margin classifier.
Max-margin hyperplane (linear SVM)
Non-linear SVMs
Unfortunately, we often have datasets that have no separating
hyperplane.
We need to move to a non-linear solution, as we did in
moving from delta-rule learning to MLPs.
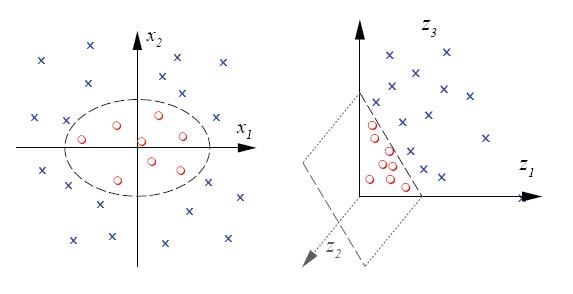
Ideally, we'd like to map the data into a feature space in
which we can form a separating hyperplane.
Separating data in a higher-dimensional space
The kernel trick
But where do we get the features for the mapping?
We'd like them to be non-linear functions (curved boundaries
are needed).
But there are infinitely many of these.
One solution is to use the so-called kernel trick.
A kernel function maps pairs of datapoints onto their inner
products (i.e., they work like distance functions).
A feature space based on a kernel function has one dimension
for every pair of datapoints.
Mathematical minimization can then be used to find the
max-margin hyperplane in the feature-space.
The effect is to identify a non-linear (curved) boundary in
the original data space.
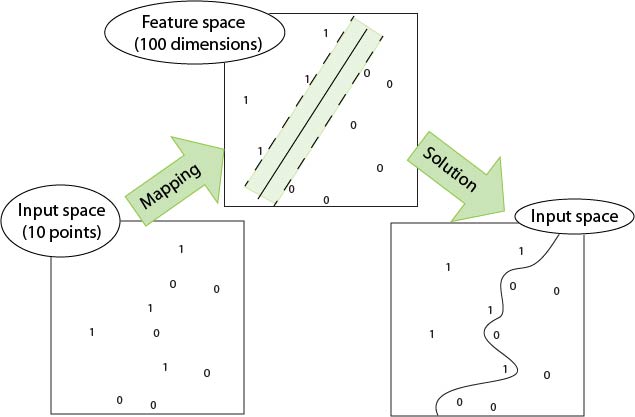
Illustration
What's really going on?
In using a kernel function, we are moving from the original
data space to a space that has one dimension for every pair
of original points.
Manipulating points in the feature space then
has the effect of
`stretching' or `compressing' areas of the data space.
This can be a way of `pulling' differently classified
datapoints apart, or `pushing' same-class points together.
Getting past the hype
SVMs using kernel functions have been getting a lot of
attention.
But their practical value remains unclear at this stage.
Derivation of weights for a separating hyperplane may still
be best done using iterative error-correction.
Key problems with SVM/kernel method
A practical problem is the leap in complexity resulting from
mapping from an dataspace containing 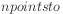 $n
\times n$ dimensional inner-product space.
$n
\times n$ dimensional inner-product space.
Another problem is the kernel function itself.
With primitive data (e.g., 2d data points), good kernels are
easy to come by.
With the forms of data we're often interested in (web pages,
MRI scans etc.), finding a sensible kernel function may be
much harder.
How would we go about defining a function that gives the
distance between two web pages?
As usual, success depends on getting the problem into the
right representation.
Summary
- Max-margin classifiers can be derived by minimization.
- Kernel-based SVMs
- Complexity problems
- The difficulty of finding good kernel functions.
Questions
- In what ways might we calculate the distance (dissimilarity)
between web pages?
- In the SVM method, we distort the data space so as to enable
simple (e.g., hyperplane-based) representation of the target
function. Can the components of the distortion be viewed as genuine
features?
- How is generalization performance likely to be affected, where
the SVM produces a high degree of data-space distortion?
Further reading
New material is being generated rapidly at present. Googling
`support vector machines tutorial' or similar will produce
many interesting hits. See also
- www.kernel-machines.org
- www.support-vector.net
- Vapnik, V. (1995). THE NATURE OF STATISTICAL LEARNING THEORY. New
York: Springer.
- Vapnik, V. (2000). THE NATURE OF STATISTICAL LEARNING THEORY.
Springer.
- Vapnik, V. and Chervonenkis, A. (1971). On the uniform convergence
of relative frequencies of events to their probabilities. THEOR.
PROBAB. APPL., 16, No. 2 (pp. 264-280).




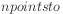 $n
\times n$ dimensional inner-product space.
$n
\times n$ dimensional inner-product space.