KR-IST - Lecture 5a Game playing with Minimax and Pruning

Chris Thornton

Introduction

An important application of AI search methods has been in the domain of 2-person games, such as draughts (checkers) and chess.

Until quite recently (late 1990s) it was widely believed by many that hard problems of intelligence would never be solved by computer.

Chess was often put forward as a good example.

Then, in May 1997, an IBM machine known as `Deep Blue' defeated chess grandmaster Garry Kasparov.

No special techniques were used to achieve the victory. Deep Blue relied on tried and trusted methods.

The version of Deep Blue which beat Kasparov was able to evalute more than 200 million chess states per second.

Kasparov and Deep Blue

Deep Blue

Recordings

Adapting search for game playing

Deep Blue used ordinary search methods. and the standard approach for adapting those methods to the problem of game-play.

Games like chess can readily be seen in terms of transitions between states. Transitions are moves; states are board configurations.

Normally, we would then solve the problem by searching for a path of transitions (i.e., moves) connecting the start state with a goal state.

Unfortunately, in this context, we `lose' control over the choice of move every other turn.

Using search for evaluation

In a 2-person game, a solution path is unobtainable because we never know what the other player is going to do at any stage.

What we need to work out is the best move.

In the minimax method we use the search process not to find a solution path, but to derive the most accurate evaluation of the possible moves, i.e., an evaluation which takes into account the implications that any given move will have later in the game.

Minimax method

There are three elements to the minimax method.

  1. Expand the search tree all the way down to a game conclusion (win, lose or draw). If this is too much search, choose a suitable cutoff.

  2. Obtain an evaluation of the relevant terminal state. (e.g., positive for a win, negative for a lose and neutral for a draw). This is known as the static evaluation.

  3. Then back-up the evaluations, level by level, working on the basis that when it is the opponent's turn, they will chose a transition which achieves the worst outcome from our point of view, and whenever it is our turn to move, we will choose the best.

To do this we need to identify the minimum evaluation in any level of the tree corresponding to the opponent's move, and the maximum otherwise.

Hence the `minimax'.

Worked example

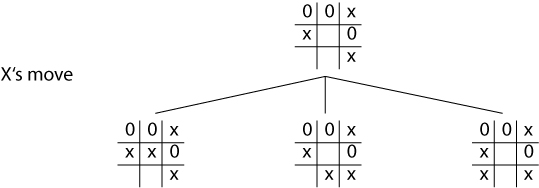
Cont.

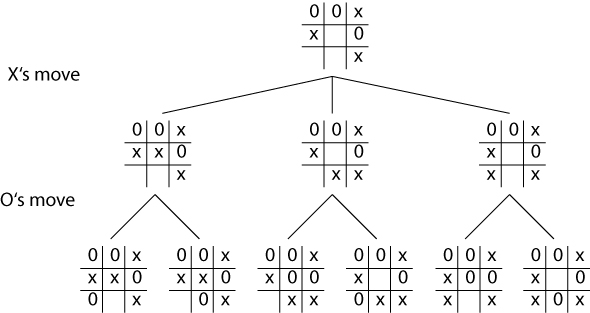
Cont.

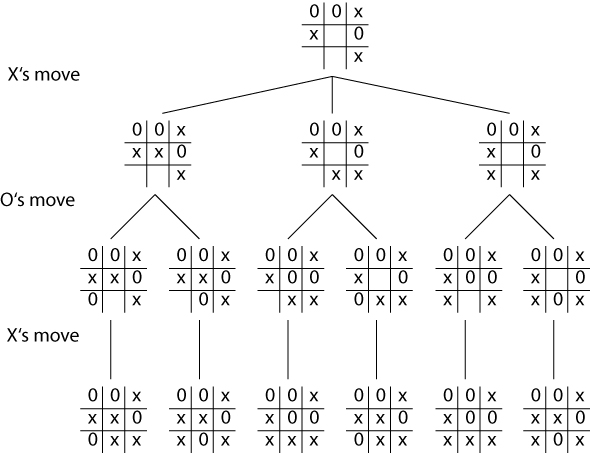
Cont.

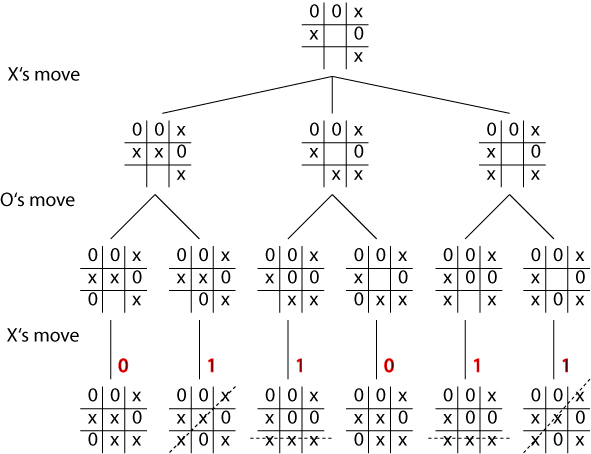
Cont.

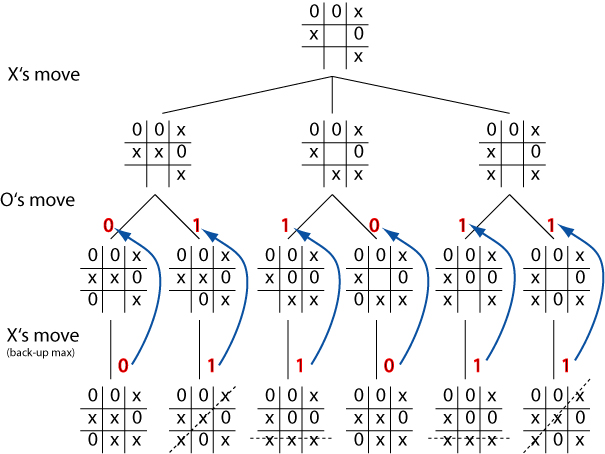
Evaluation obtained

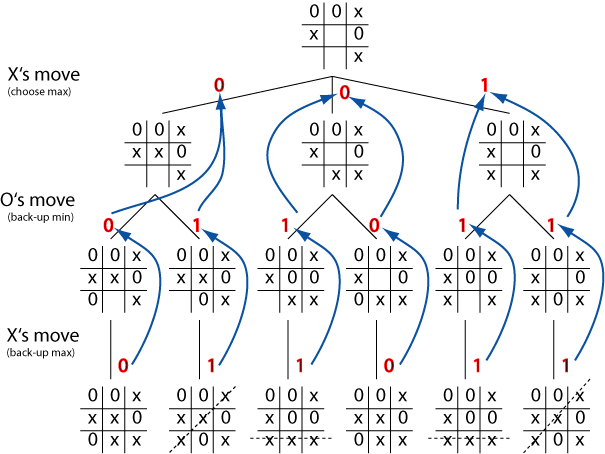
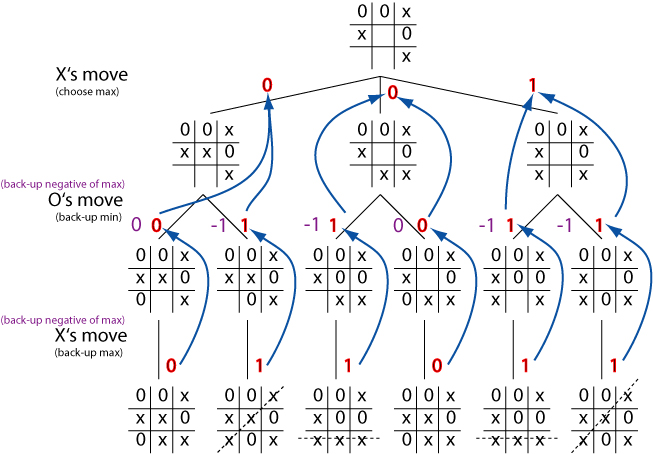
Negmax simplification

Implementing minimax can be a pain because of the need to alternate between minimisation and maximisation in the backing-up of evaluations.

The negmax idea gets around this problem.

Board states are still evaluated from the `current' player's point of view (i.e., whichever player has control at the given depth). but the value which is backed-up is always the negative of the maximum.

As in minimax, the effect is to ensure that the value backed-up is the value of the worst outcome that the opponent can achieve from our point of view.

But the code to implement the method can be written using a simple recursive procedure.

Negmax illustration

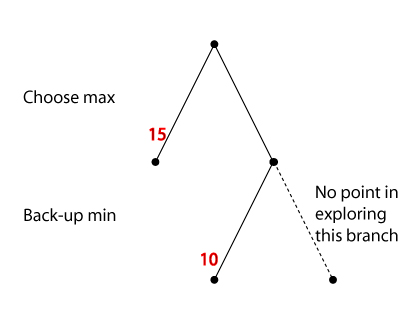
Alpha-beta pruning

When using minimax (or negmax), situations can arise when search of a particular branch can be safely terminated.

Applying both forms is alpha-beta pruning.

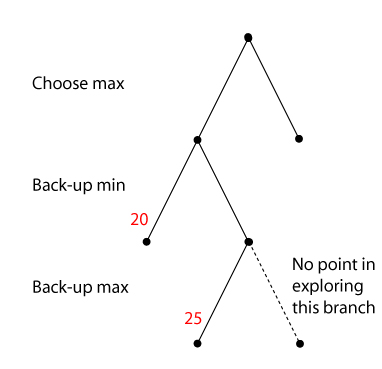
Alpha-cutoff

If, from some state S, the opponent can achieve a state with a lower value for us than one achievable in another branch. we will certainly not move the game to S. We do not need to expand S.

Beta-cutoff

If, from some state S, we would be able to achieve a state which has a higher value for us than one the opponent can hold us to in another branch, we can assume the opponent will not choose S.

.

Summary

Questions

Exercises

Exercises cont.

  X X O
  X O O
  _ _ _

Exercises cont.

Resources